【2023-08-26】
@whigzhou: 據説安慰劑效應只是一種統計假象,它源自於均值回歸,意思是,發現安慰劑效應的那些受控實驗中,接受安慰劑的受試通常都是病患,按定義,病患的健康狀況都大幅偏離均值,而隨著時間推移,即便沒有任何干預,大幅偏離均值的個體(在統計上)或多或少有向均值回歸的傾向,於是表現為安慰劑效應,
我覺得這種解釋至少對某些受控實驗可以成立,是否適用於特定某個實驗,要看具體的受試挑選方法,以及病種本(more...)
【2023-08-26】
@whigzhou: 據説安慰劑效應只是一種統計假象,它源自於均值回歸,意思是,發現安慰劑效應的那些受控實驗中,接受安慰劑的受試通常都是病患,按定義,病患的健康狀況都大幅偏離均值,而隨著時間推移,即便沒有任何干預,大幅偏離均值的個體(在統計上)或多或少有向均值回歸的傾向,於是表現為安慰劑效應,
我覺得這種解釋至少對某些受控實驗可以成立,是否適用於特定某個實驗,要看具體的受試挑選方法,以及病種本(more...)
【2022-02-20】
@yiqin_fu Kathryn Paige Harden 的书《The Genetic Lottery》总结了过去几十年关于基因和人类各种特征相关性的研究。不管是比较同异卵双胞胎、兄弟姐妹、所有人,最后算出来的这个遗传系数都比我想象中高很多(基因差异能解释形状差异的百分之几)。作者的其他几个结论是:1)系数解读要小心,因为也有社会因素。这个系数也会随着社会变化而变化;2)因果机制我们不知道;3)承认基因差别之后我们可以设计机制帮助大家(例如给近视的人戴眼镜)。
不过更大的问题仍然存在——绝大多数先天差异无法通过“戴个眼镜”这样的方案完全去掉;不同时代、不同社会奖励的技能在道德上是完全随机的。
我还特别想请教做道德哲学的朋友,有人在根据实证的这些研究重新思考 Rawls/Nozick/Friedman 的理(more...)
【2021-11-12】
今天闲着没事,再给大家讲讲性别差异这事情,
理解性别差异的最佳出发点,是下面这张图,这是两条正态分布曲线,均值都是100,蓝线的标准差是12,红线是18,(我是用 excel 的 norm.dist 函数生成的数据,然后创建了 平滑散点图,你可以动手自己试试标准差的其他值对应的形状,只需要三分钟)
我之前讲过,性别差异的许多(当然不是全部)表现都根源于禀赋分布的方差大小,而不是均值差异,男性的方差比女性大,当然,我这里取的18:12只是为了演示方便,
(当然,这里说的是认知和其他心理禀赋,若是论体能,均值差异就很大了,一个比较极(more...)
 我之前讲过,性别差异的许多(当然不是全部)表现都根源于禀赋分布的方差大小,而不是均值差异,男性的方差比女性大,当然,我这里取的18:12只是为了演示方便,
(当然,这里说的是认知和其他心理禀赋,若是论体能,均值差异就很大了,一个比较极端的例子是握力,男女的分布曲线几乎完全不重合,握力处于bottom 1%男人,其握力也比99%的女人强,)
认真看这张图,仔细琢磨,你就会理解许多现象,比如:
1)为何纯数学或理论物理这种对智商要求极高的学科里绝大多数是男人?
看右边这条虚线,如果一个领域的进入门槛是125,那么该虚线右边红蓝两条线的下方面积之比就为该领域性别比设定了基本面貌,而有些领域的门槛可能高达140,
2)为何很多行当虽然从业者多数是女人,可是其中顶尖者却多数是男人?原理相同,
3)为何随着大学普及率提高,女性比例也在不断提高,而且速度更快?
读到这里你应该已经自然懂了,当虚线处于125时,红线下面积远大于蓝线下面积,随着大学入学门槛不断降低,虚线不断向左移,女生比例逐渐提高,移到均值位置时,男女比例将趋近于入学年龄段的人口性别比,(当然,还有其他其他因素在起作用,越过入学门槛的人不一定真的入学,这里说的是背景条件),
4)为何许多性别不平等的社会,女科学家或女工程师的比例反而比性别高度平等的社会(比如北欧)更高?
因为在这些社会,科学与工程并不是最具吸引力的职业,最后侧两个标准差的那些顶尖聪明者,可能都被吸引到(比如)镇痔钻营和争权夺利事业中去了,或者争当阿亚图拉去了,诸如此类,而科学与工程领域吸引到的是均值右侧一个标准差左右的那些人,你看图中110-120之间,红蓝线下的面积大致相当,
5)上述道理是镜像适用的,就是说,当你把目光移向曲线左方,会看到与上述互为镜像的情况,即,如果一种筛选机制挑出的是最蠢、最懒、最无能、最坏、最不求上进的人,挑到的也大多是男人,比例有多高,取决于你的筛选标准的严苛程度,也就是你把虚线从左侧的红蓝交叉点往左移多远,
还有很多,留给你们自己思考吧,
我之前讲过,性别差异的许多(当然不是全部)表现都根源于禀赋分布的方差大小,而不是均值差异,男性的方差比女性大,当然,我这里取的18:12只是为了演示方便,
(当然,这里说的是认知和其他心理禀赋,若是论体能,均值差异就很大了,一个比较极端的例子是握力,男女的分布曲线几乎完全不重合,握力处于bottom 1%男人,其握力也比99%的女人强,)
认真看这张图,仔细琢磨,你就会理解许多现象,比如:
1)为何纯数学或理论物理这种对智商要求极高的学科里绝大多数是男人?
看右边这条虚线,如果一个领域的进入门槛是125,那么该虚线右边红蓝两条线的下方面积之比就为该领域性别比设定了基本面貌,而有些领域的门槛可能高达140,
2)为何很多行当虽然从业者多数是女人,可是其中顶尖者却多数是男人?原理相同,
3)为何随着大学普及率提高,女性比例也在不断提高,而且速度更快?
读到这里你应该已经自然懂了,当虚线处于125时,红线下面积远大于蓝线下面积,随着大学入学门槛不断降低,虚线不断向左移,女生比例逐渐提高,移到均值位置时,男女比例将趋近于入学年龄段的人口性别比,(当然,还有其他其他因素在起作用,越过入学门槛的人不一定真的入学,这里说的是背景条件),
4)为何许多性别不平等的社会,女科学家或女工程师的比例反而比性别高度平等的社会(比如北欧)更高?
因为在这些社会,科学与工程并不是最具吸引力的职业,最后侧两个标准差的那些顶尖聪明者,可能都被吸引到(比如)镇痔钻营和争权夺利事业中去了,或者争当阿亚图拉去了,诸如此类,而科学与工程领域吸引到的是均值右侧一个标准差左右的那些人,你看图中110-120之间,红蓝线下的面积大致相当,
5)上述道理是镜像适用的,就是说,当你把目光移向曲线左方,会看到与上述互为镜像的情况,即,如果一种筛选机制挑出的是最蠢、最懒、最无能、最坏、最不求上进的人,挑到的也大多是男人,比例有多高,取决于你的筛选标准的严苛程度,也就是你把虚线从左侧的红蓝交叉点往左移多远,
还有很多,留给你们自己思考吧,
【2020-09-06】
有关近十几年越拉越大的民调误差,我听到过两种解释:
1)调查接受度偏差,即,被访者接受或拒绝调查的几率,并不独立于其镇痔立场,保守派更可能拒绝,特别是反建制保守派,因为他们把民调机构(和主流媒体/大学/NGOs等一样)视为建制机构,并且被自由派所控制,所以更倾向于拒绝理睬,
2)投票率偏向,对于受访者,接受主动找上门的调查,成本极低,远低于大选日真正去投票的成本,而这两者间的差距在镇痔光谱上的分布并不均衡,比如,作为保守派重要票基的郊区中产,投票率远高于内城贫民,后者是自由派票基。
@_bear_:还有一个是抽样的比例。调查机构会根据历史数据预估选民的投票热情,然后定一个取样比例,比如40%左派,35右派和25%中间派,但最近选民的热情显然不同以往
@whigzhou(more...)
【2020-10-05】
@迢书 假如非要用一个指标衡量出版自由,不能用出版了多少书,而要用禁止出版了多少书。其他自由同理。
@whigzhou: 不对吧,北高丽这个指标好像是零。
@一步逃离危墙: [允悲]例外,例外
@whigzhou: 是基础假设不对,不是例外,和用『报纸天窗率』评估新闻自由度犯了同样错误
@whigzhou: 实在要设计一个单一量化指标,我看还是用『加权平均的书号成本/定价比』比较好,书号成本包括所有enab(more...)
【2020-04-09】
@whigzhou: 要想知道一个行业里是否存在网络效应,也就是会不会出现俗话所说的少数超级明星赢家通吃的局面,最简单的观察方法是看工资率的平均值与中位值的差距,因为明星效应会导致工资率分布偏离正态,至少在某个区间呈幂律分布,结果就是将均值拉高到明显超出中位值,我在新书第14章里花了两段文字讨论这个问题,下面几个数字我觉得挺有说服力:
按美国劳工部2018年的数据,若干行业小时工资率的均值与中位值对比:
演员:$29.34 v. $17.54,差67%
播音员:$24.82 v. $1(more...)
【2019-01-29】
@polyhedron You can be a professional basketball player, no matter how tall you are!
No correlation between height and scoring success in the NBA:
在NBA中,身高和場均得分數不存在相關性。(這是一個非常好且典型的相關性解釋題。)
@whigzhou: 这逻辑错的有点惊世骇俗(more...)
 在NBA中,身高和場均得分數不存在相關性。(這是一個非常好且典型的相關性解釋題。)
@whigzhou: 这逻辑错的有点惊世骇俗了~原图中的数据只能支持『同级球队中个体球员的表现与其身高无关』,远远不是『任一个体成为好球员的可能性与其身高无关』。
@whigzhou: 假设身高确实是篮球运动的重要优势,那么矮个球员就需要其他方面的优异禀赋来补偿身高劣势,这一补偿的结果,完全可能产生原图的数据
@慕容飞宇gg:类似的一个错误论证,有人否定十万小时定律的论证是:专家水平的高低和学习时间无相关性所以能不能成为专家和学习时间无关。
在NBA中,身高和場均得分數不存在相關性。(這是一個非常好且典型的相關性解釋題。)
@whigzhou: 这逻辑错的有点惊世骇俗了~原图中的数据只能支持『同级球队中个体球员的表现与其身高无关』,远远不是『任一个体成为好球员的可能性与其身高无关』。
@whigzhou: 假设身高确实是篮球运动的重要优势,那么矮个球员就需要其他方面的优异禀赋来补偿身高劣势,这一补偿的结果,完全可能产生原图的数据
@慕容飞宇gg:类似的一个错误论证,有人否定十万小时定律的论证是:专家水平的高低和学习时间无相关性所以能不能成为专家和学习时间无关。
【2018-03-12】
@果壳 【理工班=和尚班?为什么理工女成了“稀有物种”?】“你们机械班有多少男生?我没问你总人数,哦,男生人数就是总人数了……”在理工专业、学院、大学,女生一直被当作“稀有物种”。有的专业有几百号人,可女生的人数还没占个零头。为什么?一些人认为是女生的理科不如男生,事实真的如此吗? °理工科的女生为什么少?因为她们理科差?
@李子李子短信: 女性的理工科成绩不比男性差,但是阅读普遍更好,很多是基于个人优势和兴趣方面的选择。
@whigzhou: 总体看女性的理工科成绩不比男性差,但男性的方(more...)
【2018-03-08】
@黄亚生:《黄亚生:一个致命的决定》2月14日,美国佛罗里达州再次发生严重的校园枪击案。一名名叫王孟杰的15岁华裔少年在枪击发生时,为了保护其他的学生和老师,舍……
@innesfry: 佛罗里达人均GDP排名40,纽约排名第2,为什么不是从富的地方搬到穷地方枪击风险/暴力犯罪风险增加了?
@whigzhou: 最可笑的是反枪党总是用gun death来比较评价枪政,为啥不算算bed和bed death的关系?把bed禁(more...)
【2016-07-25】
@whigzhou: 以统计学方法为主导的研究有个问题是,容易让人忽视一些有着根本重要性但又缺乏统计差异的因素,比如身高,在一个儿童营养条件普遍得到保障的社会,研究者可能会得出『营养不是影响身高的重要因素』的结论,并且这一结论可能在很多年中都经受住了考验,直到有一天,某一人群经历了一次严重营养不良……
@whigzhou: 在可控实验中,此类问题可以通过对营养条件这一参数施加干预而得以避免,但社会科学领域常常不具备对参数进行任意干预的条件,只能用统计学方法来模拟可控实验,可是(more...)
Tails of Great Soccer Players
伟大足球运动员的窄尾分布
作者:Jacob @ 2015-11-19
译者:Veidt(@Veidt)
校对:Drunkplane(@Drunkplane-zny)
来源:Put A Number On It!,http://putanumonit.com/2015/11/10/003-soccer1/
Isn’t it strange that the Chinese aren’t world champions in every single team sport? Here’s why it’s strange: China has 19% of the world’s population. For individual sports that may not be a huge deal: if tennis ability and opportunity are distributed equally around the world, there would be only a 19% chance that the best tennis player hails from China and 81% that he is Swiss, Serbian, Spanish, Scottish or from any other country. It is somewhat surprising seeing the top 5 superior servers and strikers of soft springy spheres with swings of stringed racquets all come from sovereign states that start with “S”, but that’s a separate story.
中国没能在所有团队运动项目中成为世界冠军着实是件奇怪的事情。这之所以奇怪,是因为中国拥有着全世界19%的人口。对于个人运动项目来说,也许这个数字还并不算太大:如果打网球的能力和机会在全球均等地分布,那么全世界最好的网球运动员来自中国的概率仅有19%,而他来自于瑞士,塞尔维亚,西班牙,苏格兰或者任何其它国家的概率则有81%。全世界最具统治力的5名网球选手都来自于国名以“S”开头的国家这件事情的确有点令人吃惊,但那是另一件事情。
In team sports that should be different. If soccer talent was equally spread China should have on average 19 of the top 100 players in each generation, almost never less than 11. Countries like Spain, Germany and France on the other hand would expect to have 1 player in the top 100, maybe 2 or 3 if they’re lucky. That would be no match for the loaded Chinese squad. Even a top 3 player can’t dominate all by himself in a team-based sport like soccer, as evidenced by the below picture of sad Ronaldo.
在团队运动中情况则完全不同。如果踢足球的天赋在世界上均等地分布,那么平均而言,在每一代世界上最好的100名球员中,中国会拥有19个,而这个数字几乎绝不可能低于11。另一方面,西班牙,德国和法国这些国家则通常只会有1名球员进入全球前100名,即使幸运的话也最多只有2或3名。而他们的队伍应该完全无法与皆由精英组成的中国队抗衡。毕竟,即使是排名世界前3的球员也无法在足球这样的一项团队运动中靠一己之力统治比赛,下图中C罗悲伤的表情充分证明了这一点。
And yet, the Chinese team is not good at soccer, and I’m putting that milder than some. The Chinese men’s national soccer team is ranked 84th in the world, a few spots below Antigua and Barbuda – a nation with a population of 90,000. That’s roughly equal to a single neighborhood in Shanghai.
但实际上中国足球队的水平并不高,而我的这种表述方式已经比一些人温和得多了。中国男子国家足球队的世界排名是第84位,他们的积分比安提瓜和巴布达还要低上几分,而这个国家的人口仅有9万,几乎只相当于上海的一个街区。
Motivation is often brought up as an explanation: perhaps the Chinese have the talent and opportunity to play soccer, but all 1.3 billion of them choose not to. Perhaps instead of playing soccer they choose to study. Those that play soccer the least and study the most can go into medicine, and those that study hardest of all and have no room for soccer make it into top medical schools in the US.
常被提到的一个理由是动力不足:也许中国人拥有踢足球的天赋和机会,但是13亿中国人却选择不去踢。也许他们宁愿把时间花在学习上。那些踢球踢得少,读书读得多的孩子可以去学医,而那些在学习上最用功以至完全没时间踢球的(more...)
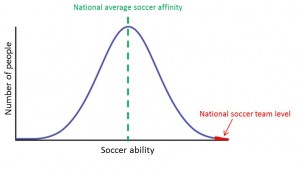 If we imagine that soccer affinity is normally distributed, a country’s population is the size of the bell curve and the national affinity is how far to the right on the ability axis the center of the bell curve is. The level of a country’s national team is how far on the ability axis the best 11 men and women are.
如果我们假设“足球亲和性”这个因子服从正态分布,一国的人口就是钟形曲线的面积,而一个国家的“足球亲和性”则可以被定义为钟形曲线的中心线在能力轴上的投影与原点之间的距离。而该国国家队的水平则取决于该国最优秀的11名男球员和女球员在能力轴上所处的位置。
Clearly, having a larger bell curve (more people at every level of play) and shifting the curve to the right (better players on average) should both contribute to boosting the level of the national team. The fact that there are over 15,000 Chinese for each Antiguan, and yet the soccer teams are comparable in level, presents the following puzzle:
很显然,拥有一个面积更大的钟形曲线(在各种水平上都拥有更多的人口)以及让钟形曲线向右移动(更高的球员平均水平)都有助于提升一国国家队的水平。而中国的人口是安提瓜人口的15000倍,但这两国的国家队水平却处于同一档次这一事实则向我们提出了如下的难题:
Why does it seem that national team level depends on affinity much more than on population?
为什么国家足球队的水平对“足球亲和性”的依赖程度要远远高于对人口的依赖程度?
The answer to that puzzle is: Because the tails of a normal distribution fall much faster than you think.
而这个问题的答案是:因为一个正态分布的尾部下降的速率比你想象的要快得多。
In plain(er) English: every point on a bell curve is some distance away from the middle (the mean). The further away from the mean you go the less points there are (lower curve). These distances are often measured in standard deviations, or SD, shown by the vertical red lines on the picture. On a standard bell curve, just over 68% of the points are found a distance of less than 1 SD from the mean in either direction.
更直白的就是:钟形曲线上每个点和中心(也就是平均值)都存在一个距离。与平均值的距离越远,这个水平上的点数也就越少(在曲线上就越低)。而与中心的距离通常是以标准差计的(在图中用红色的垂直线条表示)。在一个标准的钟形曲线上,有68%的点都会落在均值两端一个标准差的距离之内。
If we imagine that soccer affinity is normally distributed, a country’s population is the size of the bell curve and the national affinity is how far to the right on the ability axis the center of the bell curve is. The level of a country’s national team is how far on the ability axis the best 11 men and women are.
如果我们假设“足球亲和性”这个因子服从正态分布,一国的人口就是钟形曲线的面积,而一个国家的“足球亲和性”则可以被定义为钟形曲线的中心线在能力轴上的投影与原点之间的距离。而该国国家队的水平则取决于该国最优秀的11名男球员和女球员在能力轴上所处的位置。
Clearly, having a larger bell curve (more people at every level of play) and shifting the curve to the right (better players on average) should both contribute to boosting the level of the national team. The fact that there are over 15,000 Chinese for each Antiguan, and yet the soccer teams are comparable in level, presents the following puzzle:
很显然,拥有一个面积更大的钟形曲线(在各种水平上都拥有更多的人口)以及让钟形曲线向右移动(更高的球员平均水平)都有助于提升一国国家队的水平。而中国的人口是安提瓜人口的15000倍,但这两国的国家队水平却处于同一档次这一事实则向我们提出了如下的难题:
Why does it seem that national team level depends on affinity much more than on population?
为什么国家足球队的水平对“足球亲和性”的依赖程度要远远高于对人口的依赖程度?
The answer to that puzzle is: Because the tails of a normal distribution fall much faster than you think.
而这个问题的答案是:因为一个正态分布的尾部下降的速率比你想象的要快得多。
In plain(er) English: every point on a bell curve is some distance away from the middle (the mean). The further away from the mean you go the less points there are (lower curve). These distances are often measured in standard deviations, or SD, shown by the vertical red lines on the picture. On a standard bell curve, just over 68% of the points are found a distance of less than 1 SD from the mean in either direction.
更直白的就是:钟形曲线上每个点和中心(也就是平均值)都存在一个距离。与平均值的距离越远,这个水平上的点数也就越少(在曲线上就越低)。而与中心的距离通常是以标准差计的(在图中用红色的垂直线条表示)。在一个标准的钟形曲线上,有68%的点都会落在均值两端一个标准差的距离之内。
 Looking naively at the familiar bell picture, it seems that the curve drops sharply over the first 2 or 3 SD to either side and then levels off around 0 when you move further away. That’s extremely misleading: the relative height of the curve actually drops faster the further out you go. It’s invisible on the chart because the line further than 3 SD out is squished very close to 0. The height of the curve at 1 SD is 4.5 times higher than that at 2 SD. The curve at 5 SD is 250 times higher than that at 6 SD and it keeps getting steeper and steeper.
如果我们直观地看一下这条熟悉的钟形曲线,看起来曲线两端在距离中心最初的两三个标准差内下降得非常快,而在之后更远的距离上就会在零附近以一种接近水平的方式缓慢下降。而这实际上会造成巨大的误导:事实上,距离中心越远,曲线的相对高度下降的速度越快。但由于在3个标准差之外,曲线被压缩到了非常接近0的高度,所以在图上我们看不到。曲线上1标准差处的高度是2标准差处的4.5倍,而5标准差处的高度则是6标准差处的250倍,而随着离中心越来越远,曲线的陡峭程度还在不断上升。
The best male soccer player in China (Zheng Zhi?) is almost literally one in a billion, which means that he’s almost 6 standard deviation better than the average Chinese. If the population of China doubled (they’re working on it!), there would be 2 players as good as Zheng is. However, if the population of China became just one standard deviation better at soccer, there would be over 200 players at least as good, and a few dozen who are much better.
中国最好的男性球员(是郑智吗?)在中国差不多是十亿里挑一了,这意味着他的水平比中国人的平均足球水平要高6个标准差。如果中国的人口增加一倍(他们的确在努力这么干!),那么中国将会出现两个和郑智一样优秀的球员。然而,如果中国人的平均足球水平能够提高一个标准差的话,那么中国就会有超过200名球员和郑智水平一样高了,而且还会有几十名球员的水平比他高得多。
It could be that a normally distributed soccer skill model is wholly wrong, but it does seem to explain some of what we see in reality. For anything that’s distributed roughly like a bell curve, the quality of the best people in a large enough group (like a country) depends much more on small differences in the average level than on large differences in total population. Hey, I wonder if that’s why so many Nobel prize winners are… *gets repeatedly electrocuted*
实际上这个正态分布的足球水平模型可能是完全错误的,但是它看起来的确解释了一些我们在现实中观察到的现象。对于任何一个分布接近钟形曲线的群体,在一个足够大的群体(比如一个国家)中,水平最高者的能力更多地取决于平均水平上的微小差异,而人口总数上的巨大差异所发挥作用则要小得多。嘿,现在我开始怀疑这就是为什么如此多的诺贝尔奖得主都死于触电的原因了。
Whoops, sorry about that. Let’s see this effect in action on the one trait that we can all agree is close to normally distributed and varies among nations: human height.
抱歉这个梗有点欠。让我们通过一个特征来看看这种效应的实际力量,该特征的近似正态分布得到了大家认可,而且在国家间存在差异:那就是人的身高。
The average Indian dude (sorry for the androcentrism, ladies, there’s just better data on male heights and male soccer teams) is 165 cm (5′ 5″) and there are roughly 630 million of them. The average Norwegian dude is 180 cm (5′ 11″) and there are 2.5 million. The standard deviation of male height is around 6 cm around the world. If heights were distributed in a perfect normal bell curve with those parameters they would look like:
印度6.3亿成年男性(女士们,抱歉了,这里看起来似乎有点大男子主义,但有关男性身高和男子足球队的数据质量的确更好)的平均身高是165厘米(5英尺5英寸)。而挪威250万成年男性的平均身高则是180厘米(5英尺11英寸)。全世界身高的标准差大约是6厘米。如果身高完全服从一个由这些参数构建的正态钟形分布,那么看起来将会像下图这样:
Looking naively at the familiar bell picture, it seems that the curve drops sharply over the first 2 or 3 SD to either side and then levels off around 0 when you move further away. That’s extremely misleading: the relative height of the curve actually drops faster the further out you go. It’s invisible on the chart because the line further than 3 SD out is squished very close to 0. The height of the curve at 1 SD is 4.5 times higher than that at 2 SD. The curve at 5 SD is 250 times higher than that at 6 SD and it keeps getting steeper and steeper.
如果我们直观地看一下这条熟悉的钟形曲线,看起来曲线两端在距离中心最初的两三个标准差内下降得非常快,而在之后更远的距离上就会在零附近以一种接近水平的方式缓慢下降。而这实际上会造成巨大的误导:事实上,距离中心越远,曲线的相对高度下降的速度越快。但由于在3个标准差之外,曲线被压缩到了非常接近0的高度,所以在图上我们看不到。曲线上1标准差处的高度是2标准差处的4.5倍,而5标准差处的高度则是6标准差处的250倍,而随着离中心越来越远,曲线的陡峭程度还在不断上升。
The best male soccer player in China (Zheng Zhi?) is almost literally one in a billion, which means that he’s almost 6 standard deviation better than the average Chinese. If the population of China doubled (they’re working on it!), there would be 2 players as good as Zheng is. However, if the population of China became just one standard deviation better at soccer, there would be over 200 players at least as good, and a few dozen who are much better.
中国最好的男性球员(是郑智吗?)在中国差不多是十亿里挑一了,这意味着他的水平比中国人的平均足球水平要高6个标准差。如果中国的人口增加一倍(他们的确在努力这么干!),那么中国将会出现两个和郑智一样优秀的球员。然而,如果中国人的平均足球水平能够提高一个标准差的话,那么中国就会有超过200名球员和郑智水平一样高了,而且还会有几十名球员的水平比他高得多。
It could be that a normally distributed soccer skill model is wholly wrong, but it does seem to explain some of what we see in reality. For anything that’s distributed roughly like a bell curve, the quality of the best people in a large enough group (like a country) depends much more on small differences in the average level than on large differences in total population. Hey, I wonder if that’s why so many Nobel prize winners are… *gets repeatedly electrocuted*
实际上这个正态分布的足球水平模型可能是完全错误的,但是它看起来的确解释了一些我们在现实中观察到的现象。对于任何一个分布接近钟形曲线的群体,在一个足够大的群体(比如一个国家)中,水平最高者的能力更多地取决于平均水平上的微小差异,而人口总数上的巨大差异所发挥作用则要小得多。嘿,现在我开始怀疑这就是为什么如此多的诺贝尔奖得主都死于触电的原因了。
Whoops, sorry about that. Let’s see this effect in action on the one trait that we can all agree is close to normally distributed and varies among nations: human height.
抱歉这个梗有点欠。让我们通过一个特征来看看这种效应的实际力量,该特征的近似正态分布得到了大家认可,而且在国家间存在差异:那就是人的身高。
The average Indian dude (sorry for the androcentrism, ladies, there’s just better data on male heights and male soccer teams) is 165 cm (5′ 5″) and there are roughly 630 million of them. The average Norwegian dude is 180 cm (5′ 11″) and there are 2.5 million. The standard deviation of male height is around 6 cm around the world. If heights were distributed in a perfect normal bell curve with those parameters they would look like:
印度6.3亿成年男性(女士们,抱歉了,这里看起来似乎有点大男子主义,但有关男性身高和男子足球队的数据质量的确更好)的平均身高是165厘米(5英尺5英寸)。而挪威250万成年男性的平均身高则是180厘米(5英尺11英寸)。全世界身高的标准差大约是6厘米。如果身高完全服从一个由这些参数构建的正态钟形分布,那么看起来将会像下图这样:
 As we plot them side by side, the Indian curve completely dwarfs the Norwegian one, even for pretty tall dudes. There are 9 Indians who are exactly 180 cm (5′ 11″) tall for every Norwegian. 5′ 11″ is tall, but not super tall. The higher mean effect only kicks in for the real outliers, so let’s zoom the above plot in to the really tall dudes.
当我们把整个分布画在一起,印度的曲线看起来完全压倒了挪威的曲线,即使对于身高很高的成年男性也是这样。印度和挪威身高180(5英尺11英寸)厘米的人口数量比例是9比1。5英尺11英寸算是高了,但并不是非常高。高均值效应只有在那些真正的异常值上才会起作用,那么让我们将图上那些真的很高的成年男性所对应的部分放大看看。
As we plot them side by side, the Indian curve completely dwarfs the Norwegian one, even for pretty tall dudes. There are 9 Indians who are exactly 180 cm (5′ 11″) tall for every Norwegian. 5′ 11″ is tall, but not super tall. The higher mean effect only kicks in for the real outliers, so let’s zoom the above plot in to the really tall dudes.
当我们把整个分布画在一起,印度的曲线看起来完全压倒了挪威的曲线,即使对于身高很高的成年男性也是这样。印度和挪威身高180(5英尺11英寸)厘米的人口数量比例是9比1。5英尺11英寸算是高了,但并不是非常高。高均值效应只有在那些真正的异常值上才会起作用,那么让我们将图上那些真的很高的成年男性所对应的部分放大看看。
 Here, the picture reverses completely. There are 100 times as many Norwegians above 195 cm (6′ 4″) as there are Indians. Under a normal distribution assumption, the tallest Indian at 6′ 7″ would only match the 1,000th tallest Norwegian.
在这里,情况完全颠倒了过来。身高超过195厘米(6英尺4英寸)的成年男性数量,挪威和印度的比例是100比1。在正态分布的假设之下,印度最高的成年男性的身高将是6英尺7英寸,而这个身高在挪威人中只能排在第1000位。
It’s important to remember that a normal bell curve is a very simplistic model, real life is messy, and Dharmendra Singh is 8′ 1″. Even inside the realm of mathematics, a normal distribution has narrower tails (the height drops faster as you get away from the mean) than most other widely used distributions that look sorta like a bell curve (like the student’s t or the gamma distributions). A normal model underestimates the number of outliers and overstates the importance of shifting the mean.
我们必须记住的是,正态分布的钟形曲线是一种非常简化的模型,真实情况要复杂得多,实际上印度最高的男性Dharmendra Singh的身高是8英尺1英寸。即使在数学王国中,相比其他大多数常用的看起来像钟形曲线的分布(例如学生t分布或gamma分布),正态分布也有着窄得多的尾部(这意味着在远离均值时,曲线下降的速度更快)。一个正态分布模型会低估异常值点的数量,同时会高估平均值移动的重要性。
With that said, my main point stands: it should not surprise anyone that the achievement of extreme performers doesn’t strongly depend on the population of a country but does on the average. There doesn’t have to be something horribly wrong with China to account for its disappointing soccer team, they could be just a little bit to the left of other countries on national soccer affinity.
但即使考虑到这些情况,我的主要观点仍然成立:那些表现极端出众的个体的出现并不太依赖于一国的人口数量,而非常依赖于该国在这方面的平均水平。中国国家足球队令人失望的表现背后也许并没有什么错得离谱的东西,这也许只是因为中国在“足球亲和性”的分布上稍微靠左了一些而已。
We still don’t know what makes up soccer affinity, just that it’s enough to explain the disconnect between populations and team performance. With the math lesson behind us comes the fun part: in the next posts we’ll rank the world’s countries by average soccer affinity, throw a bunch of data at it to see what it correlates with, and see if can get any insight into what makes countries good or bad at soccer.
我们仍然不知道“足球亲和性”是由哪些因素构成的,但它足以解释人口和团队表现之间脱节的现象。在我们的这节数学课之后才是真正有趣的部分:在接下来的几篇文章中,我们将会把世界各国按照平均的“足球亲和性”进行排名,通过一系列的数据来看看它与哪些因素相关,并试着获得一些关于是什么让一个国家在足球方面表现得好或不好的深入见解。
(编辑:辉格@whigzhou)
*注:本译文未经原作者授权,本站对原文不持有也不主张任何权利,如果你恰好对原文拥有权益并希望我们移除相关内容,请私信联系,我们会立即作出响应。
Here, the picture reverses completely. There are 100 times as many Norwegians above 195 cm (6′ 4″) as there are Indians. Under a normal distribution assumption, the tallest Indian at 6′ 7″ would only match the 1,000th tallest Norwegian.
在这里,情况完全颠倒了过来。身高超过195厘米(6英尺4英寸)的成年男性数量,挪威和印度的比例是100比1。在正态分布的假设之下,印度最高的成年男性的身高将是6英尺7英寸,而这个身高在挪威人中只能排在第1000位。
It’s important to remember that a normal bell curve is a very simplistic model, real life is messy, and Dharmendra Singh is 8′ 1″. Even inside the realm of mathematics, a normal distribution has narrower tails (the height drops faster as you get away from the mean) than most other widely used distributions that look sorta like a bell curve (like the student’s t or the gamma distributions). A normal model underestimates the number of outliers and overstates the importance of shifting the mean.
我们必须记住的是,正态分布的钟形曲线是一种非常简化的模型,真实情况要复杂得多,实际上印度最高的男性Dharmendra Singh的身高是8英尺1英寸。即使在数学王国中,相比其他大多数常用的看起来像钟形曲线的分布(例如学生t分布或gamma分布),正态分布也有着窄得多的尾部(这意味着在远离均值时,曲线下降的速度更快)。一个正态分布模型会低估异常值点的数量,同时会高估平均值移动的重要性。
With that said, my main point stands: it should not surprise anyone that the achievement of extreme performers doesn’t strongly depend on the population of a country but does on the average. There doesn’t have to be something horribly wrong with China to account for its disappointing soccer team, they could be just a little bit to the left of other countries on national soccer affinity.
但即使考虑到这些情况,我的主要观点仍然成立:那些表现极端出众的个体的出现并不太依赖于一国的人口数量,而非常依赖于该国在这方面的平均水平。中国国家足球队令人失望的表现背后也许并没有什么错得离谱的东西,这也许只是因为中国在“足球亲和性”的分布上稍微靠左了一些而已。
We still don’t know what makes up soccer affinity, just that it’s enough to explain the disconnect between populations and team performance. With the math lesson behind us comes the fun part: in the next posts we’ll rank the world’s countries by average soccer affinity, throw a bunch of data at it to see what it correlates with, and see if can get any insight into what makes countries good or bad at soccer.
我们仍然不知道“足球亲和性”是由哪些因素构成的,但它足以解释人口和团队表现之间脱节的现象。在我们的这节数学课之后才是真正有趣的部分:在接下来的几篇文章中,我们将会把世界各国按照平均的“足球亲和性”进行排名,通过一系列的数据来看看它与哪些因素相关,并试着获得一些关于是什么让一个国家在足球方面表现得好或不好的深入见解。
(编辑:辉格@whigzhou)
*注:本译文未经原作者授权,本站对原文不持有也不主张任何权利,如果你恰好对原文拥有权益并希望我们移除相关内容,请私信联系,我们会立即作出响应。
——海德沙龙·翻译组,致力于将英文世界的好文章搬进中文世界——
Top 1%, across states
最富有的1%,州与州间的比较
作者:Salil Mehta @ 2015-1-31
译者: 一声叹息 校对:小册子(@昵称被抢的小册子)
来源:Statistical Ideas,http://statisticalideas.blogspot.com/2015/01/top-1-across-states.html
Short-term update: this article has been fancied by some of the country’s most esteemed economists and featured in popular outlets such as Marginal Revolution (by a frequent NYT Upshot writer), supported by EconLog’s Arnold Kling, favorably tweeted by research head at Oxfam, and aknowledged by the Deans of three schools (one in public policy, and two in business). Within the first day generated >100 facebook shares, and >100 tweets, from various media here.
近期动态:本文深受本国一些声誉卓著的经济学家的喜爱,被“边际革命”等流行站点作为专题文章推荐。本文也得到了来自EconLog的Arnold Kling的大力支持,被乐施会的研究院领导热情转发,并得到三个学院(一个公共政策学院,两个商学院)院长的认可。本文发出第一天,就被这里的媒体在Facebook上分享100多次,在Twitter上推送100多次。
It’s an appealing chart from this week’s Economic Policy Institute’s report, leveraging the fashionable, French economist Piketty’s statistics, in order to illustrate how well the “top 1%” are doing in each of the 50 states. The report is provokingly titled: “The Increasingly Unequal States of America”.
经济政策研究所(EPI)本周的一份报告中,给出了一张富有吸引力的图表,引用了法国新潮的经济学家皮凯蒂的统计资料,用以说明“最富有的1%”在每个州过得有多滋润。这份报告有个煽动性的标题:美利坚大不平等国。
But the report creates distortions in the truth. An important matter affecting hundreds of millions should also include a straight acknowledgement of probability theory. We see through this article, that beyond the obvious national-level inequality (those at the top versus those at the bottom), targeting s(more...)
——海德沙龙·翻译组,致力于将英文世界的好文章搬进中文世界——
【2015-08-11】
@海德沙龙 【焦点议题】有关贫富差距的数字常令公众大吃一惊,但许多抓人眼球的惊人“差距、变化”,其实往往是统计假象,其背后根本没有人们以为它所揭示的事实,同一组数据,平凡还是惊艳,更多取决于如何组织和表述它,本文分析了其中一例,今后我们还会介绍更多 http://t.cn/RLmCHik
@whigzhou: 所以在对统计数字发出感慨之前,最好先弄清楚统计指标是怎么设计的,然后再想想差异或变化到底是不是你打算感叹的那个因素造成的。举个简单例子,假如(more...)
【2012-12-24】
@P_Slacker:美国康奈尔大学的一项调查称:容易相处的员工,薪酬明显低于脾气不太好的员工。
@宮鈴_胡同台妹: 這是要大家脾氣壞一點嗎?
@局外人c的空间 应该的,所谓“二球”,在中国就很占便宜。请教@高利明 @whigzhou
@whigzhou: 这种事情最好做跟踪研究,仅凭几个数字你不知道究竟发生了什么
@whigzhou: 可能之一:脾气差的晋升慢,因而比同等职位者年资长,所以工资高;可能之二:脾气差的失业率高,但没失业那些工资也偏高;可能之三:脾(more...)