题:平面内,由若干相邻全等正六边形组成蜂窝网络,其中部分蜂窝为深色,其余为浅色,问:深色蜂窝如何分布可满足如下条件?此时深浅色蜂窝比例为多少?
1)每个深色蜂窝被6个浅色蜂窝围绕,
2)不可能将任何浅色蜂窝改为深色,而继续满足条件(1)。
题目不难,大概算初中程度,不过之前确实没想过,昨天读施坚雅(G.W. Skinner)的《中国农村的市场和社会结构》才遇到这问题,而且答案与直觉还有点出入。
施坚雅在该书中提出的蜂窝模型(姑且这么叫吧)大名鼎鼎,如雷贯耳,不过读了原著还是发现比以前听说和想象的更精致巧妙的多,是社会结构自组织(或曰自发秩序)的一个精彩案例,该模型中基本的单位是“基层市场”(蜂窝),其标准配置是1个基层集镇和围绕它18个村庄,这些村庄组成两个环,内环6个,外环12个,从集镇辐射出6条小路,通往这些村庄。
蜂窝比较简单,但蜂窝之间的组合就颇为复杂,面临两个结构问题,首先,相邻蜂窝之间会发生分化,其中一些集镇会升级为二级集镇,为周边市场提供后者无法提供的市场功能,如批发和中介服务、需求量较小的商品和服务等,典型的二级集镇由6个基层集镇所围绕,它们共同组成一个二级市场,问题是:如何围绕法?具体的空间分布是怎样的?(这就是上面的题目所问的)
其次,传统集市大多不是每天开市,而是按某种频率隔几天开一次,即所谓“集期”(period of market),比如“逢一市”就是每旬第一天开市,“一六市”每旬开两天,还有“一四七”“二五八”等等;如此安排,一是因为集市所覆盖范围内交易量太小,无须每天开市,二是因为单一集市的交易规模不足以支撑许多生意类别,多个相邻集市轮流开市可以让行商每天有生意可做,问题是:各相邻集市之间如何协调集期?
对第二个问题,施坚雅发现,每个新开基层集市只须依此遵循下列规则,系统便可达致理想结构:
1)首先,避开邻近上级集市的集期;
2)其次,避开邻近基层集市的集期;
3)若有可能,也避开同一二级市场的其他基层集市的集期;
施坚雅用几个例子演示了,最终形成的轮转方式颇为精妙,细节我这儿不描述了,有兴趣的同学可以去看书。
至于第一个问题,或许你已想出答案了,如下图,有三种可能(从左到右分布为A、B、C),疏密不同,对应的深浅蜂窝比例分别为:1:4,1:3,1:6,和你的直觉吻合吗?对比经验数据之后,施坚雅发现,第三种情况(C)实际上不存在,而A和B都很常见,A多见于单位土地产出较低、人口稀疏、交通不便的地区,而B多见于单产高、人口密集的平原地区,其中原因,并不如看上去那么简单(直观上B就比A紧密),说起来比较绕口,还是请看原著吧。

 订阅
订阅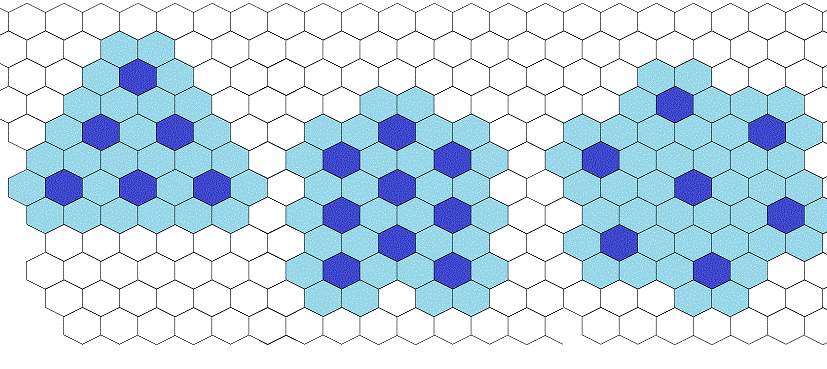
??? @ 2011-07-22, 16:51
跑题一下:在GoogleReader上看到题目的瞬间,我还以为穿越到Matrix67了……
[回复]
zhang3 回复:
7月 22nd, 2011 at 17:09
同上
[回复]
辉格 回复:
7月 22nd, 2011 at 19:10
哈,人家那可是奥数水平,我这个学前儿童都能摆弄
[回复]
gaohan_cn 回复:
7月 25th, 2011 at 16:40
您这样过于自谦,严重伤害了我的感情。。。
[回复]
tcya @ 2011-07-24, 07:57
刚在辉总的豆瓣逛了逛,看到对《契约论》的评价。。。我看那书也完全看不下去,但我觉得是自己的问题。。因为我看其他好书也经常看不下去,辉总能说说那书肿么了吗
[回复]
辉格 回复:
7月 25th, 2011 at 14:38
假如你在读一本号称是关于社会的书,里面的词汇语句却很少能唤起你对社会现实的印象,那要么是作者在凭空意淫,要么是你阅历不够,无论哪种情况,都没必要再读下去了,对吧?
[回复]
tcya 回复:
7月 25th, 2011 at 14:45
但是我觉得把人与人、人与政府的关系理解为一种契约还挺好用的,不过这种看法是我从网文里学来的,当初就是觉得这想法解释问题还挺好用才想着去看原著,结果至今我也不知道卢梭原意是不是这样,因为那书我实在看不进去。。
[回复]
tcya 回复:
7月 25th, 2011 at 14:51
辉总觉得社会契约这理论本身就挺糟糕吗,还是书写的差?我对社会契约的理解很肤浅,大概就是大家可以不要政府的,是人们自愿达成契约来雇个政府做事,所以依据契约人们有什么什么样的权利。我知道这很不符合历史,但是这理论拿来跟别人解释人民对政府可以怎么怎么样还是挺简洁的
[回复]
辉格 回复:
7月 25th, 2011 at 15:36
1)基于契约(而非强制)的制度当然是理想的——至少对我这样的无政府主义者来说,但实际上,历史上的政府制度很少是基于契约的,只有封建制中包含了一些契约元素,所以,用契约理论来解释制度发展是很不靠谱的;
2)卢梭用“契约”二字来谈论的那些东西,我压根看不出任何与契约有关的痕迹;
[回复]
blindc 回复:
7月 25th, 2011 at 18:07
契约这词太空,可以套进去的东西太多,容易把自己绕沟里面
要把人和人自发组成的制度从卢梭的套套逻辑里分辨出来,还是需要一些实证读物的,至于人和政府达成契约,就完全不靠谱了
[回复]
limln @ 2016-01-14, 19:33
想到了伯努利的“错放信封”问题:如果要将n封信放入n写有地址的信封中,那么每一封信放错的概率是多少呢?答案是1/e。数论中的质数分布密度也是1/e。果然自然对数的底才可以这么自洽
[回复]